REPRO Fun!
CSJP

# set a seed for reproducible results
set.seed(1234)
# toss a coin
sample(c("H", "T"), 10, replace = TRUE)## [1] "H" "T" "T" "T" "T" "T" "H" "H" "T" "T"# roll a die
sample(1:6, 10, replace = TRUE)## [1] 5 4 2 6 2 6 2 2 2 2# roll 2 dice
dice = as.vector(outer(1:6, 1:6, paste))
sample(dice, 5, replace = TRUE)## [1] "6 2" "5 2" "6 1" "2 1" "2 2"# pick 6 of 54 - lottery
sample(1:54, 6)## [1] 44 28 48 43 3 23# play a card - a pair of jacks
cards = paste(rep(c("A", 2:10, "J", "Q", "K"), 4), c("H", "D", "S",
"C"))
sample(cards, 5)## [1] "A D" "3 C" "K D" "9 H" "J H"
# significant levels
alphas <- c(0.01, 0.05, 0.1, 0.32, 0.62)
# new function to plot significant levels with std. normal dist.
siglplot(alphas)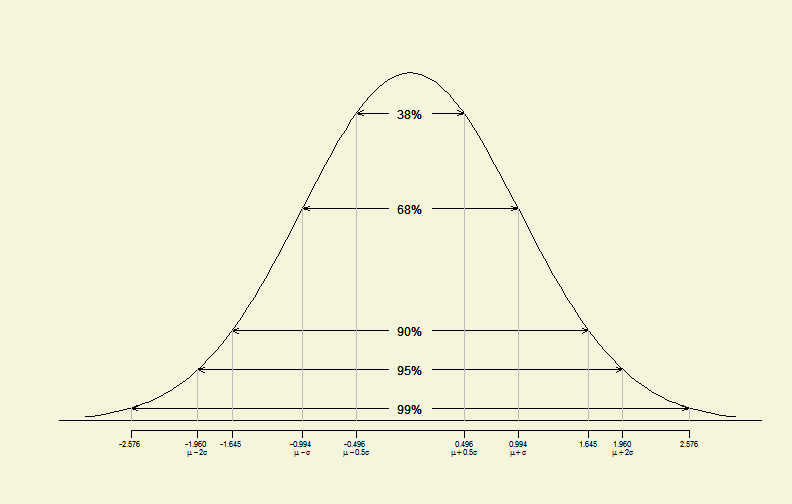
Standard Normal Distribution
# 2-sample - paired & !var.equal
x1 <- c(36.7, 35.8, 31.9, 29.3, 28.4, 25.7, 24.2, 22.6, 21.9, 20.3)
x2 <- c(36.2, 35.7, 32.3, 29.6, 28.1, 25.8, 23.9, 22, 21.5, 20)
# new function created by my own confidence :)
out <- ci.t(x1, x2, paired = TRUE, conf.level = c(0.9, 0.95, 0.99))
# using xtable to automatically generate a table as below:| CI.lower | CI.upper | |
|---|---|---|
| 90% | -0.02525 | 0.36525 |
| 95% | -0.07094 | 0.41094 |
| 99% | -0.17614 | 0.51614 |
# 95% confidence intervals includes population mean assume that population
# variance is known and its distribution is normal
smpsize <- 1000
obs <- 5
pmean <- 100
psd <- 5
conf.level <- 0.95
set.seed(1234)
d <- matrix(NA, obs, smpsize)
d <- replicate(smpsize, rnorm(obs, pmean, psd))
smean <- colMeans(d)
z.value <- qnorm(1 - (1 - conf.level)/2)
cil <- smean - z.value * psd/sqrt(obs)
ciu <- smean + z.value * psd/sqrt(obs)
sum(cil < pmean & ciu > pmean)/smpsize## [1] 0.951# 1-sample - 1-side
set.seed(1234)
x <- rnorm(130, mean = 2, sd = 3)
tres <- t.test(x, mu = 1, conf.level = 0.9, alternative = "greater")
# new plot function created to plot hypo. tests
plot(tres)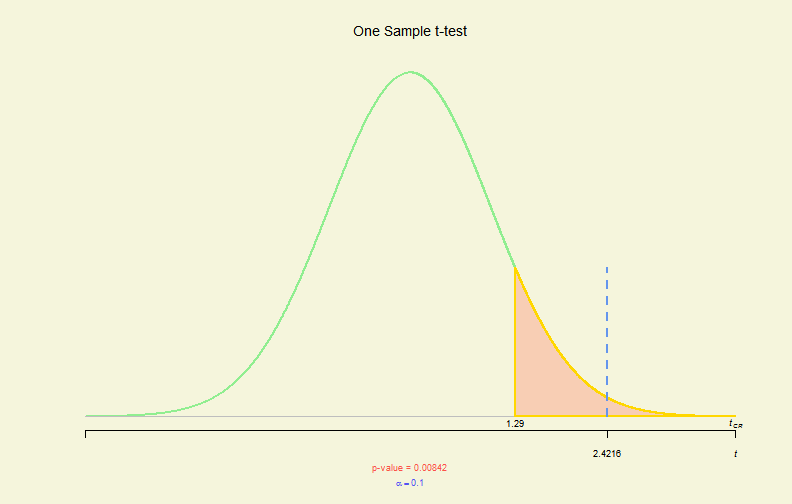
Hypo. Test Plot (I)
# 2-sample - 2- side, !paired & var.equal
myData <- read.csv("BeerWater.csv")
tres <- with(myData, t.test(B, W, var.equal = FALSE))
plot(tres)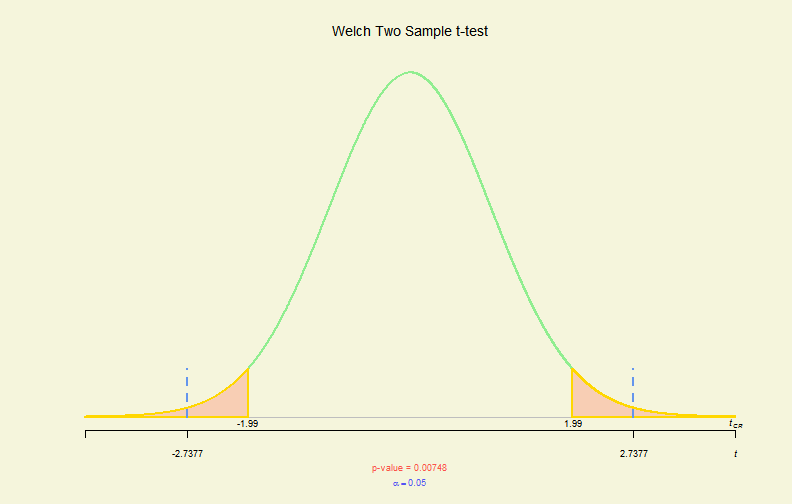
Hypo. Test Plot (II)
# 2-sample - 2-side, paired & !var.equal
x1 <- c(36.7, 35.8, 31.9, 29.3, 28.4, 25.7, 24.2, 22.6, 21.9, 20.3)
x2 <- c(36.2, 35.7, 32.3, 29.6, 28.1, 25.8, 23.9, 22, 21.5, 20)
tres <- t.test(x1, x2, paired = TRUE)
plot(tres)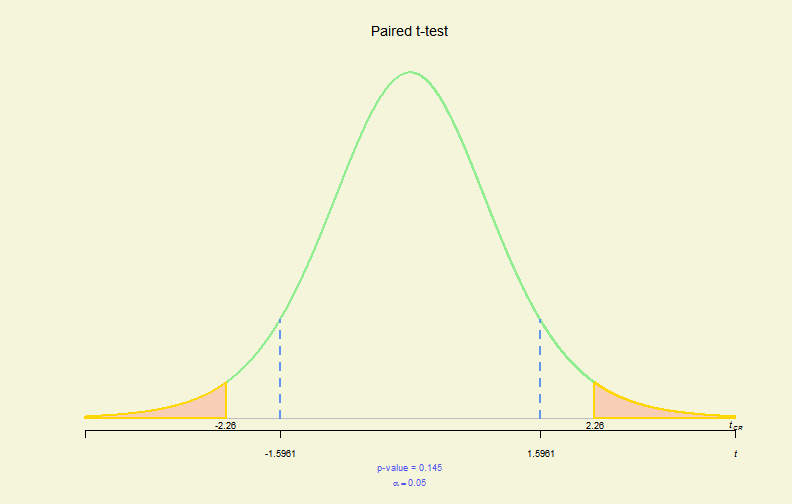
Hypo. Test Plot (III)
# 2-sample - 1-side, paired & !var.equal
x1 <- c(89, 87, 70, 83, 67, 71, 92, 81, 97, 78, 94, 79)
x2 <- c(94, 91, 68, 88, 75, 66, 94, 88, 96, 88, 95, 87)
tres <- t.test(x1, x2, alternative = "less", paired = TRUE)
plot(tres)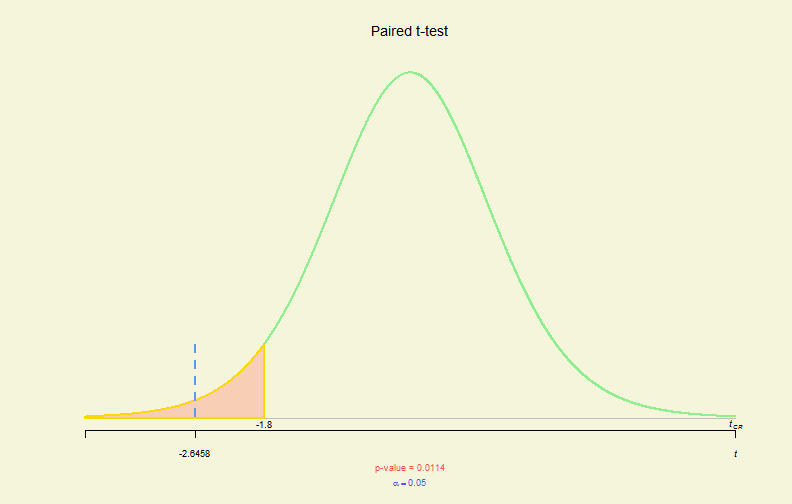
Hypo. Test Plot (IV)
# prop.test
pres <- prop.test(x = 18, n = 30, p = 0.55, alternative = "two.sided",
conf.level = 0.95, correct = FALSE)
plot(pres)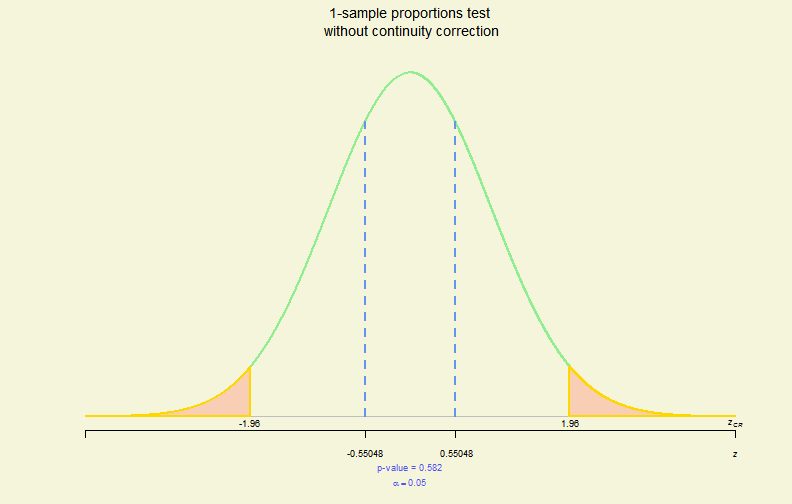
Hypo. Test Plot (V)
# var.test
myData <- read.csv("TeachingMethods.csv")
vres <- with(myData, var.test(E, L, alternative = "greater"))
plot(vres)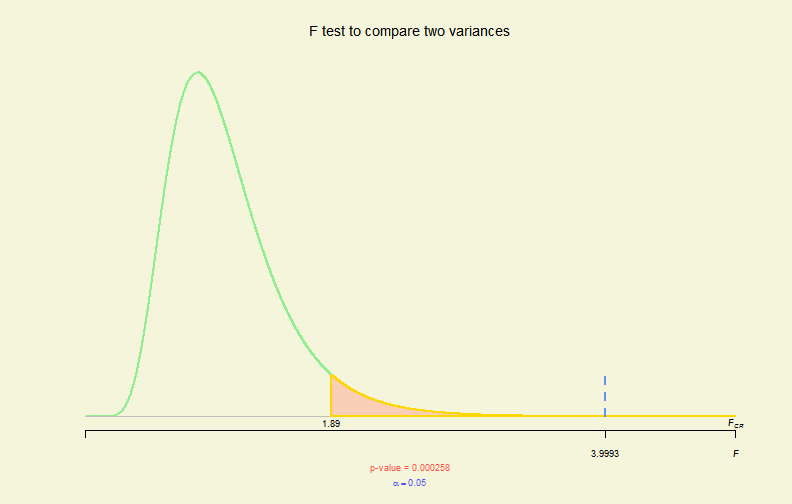
Hypo. Test Plot (VI)
# 1-sample test on a population mean
power.t.test(n = 10, d = (70 - 60), sd = sqrt(400), sig.level = 0.05,
type = "one.sample", alternative = "two.sided")##
## One-sample t test power calculation
##
## n = 10
## delta = 10
## sd = 20
## sig.level = 0.05
## power = 0.2928
## alternative = two.sided
## # 2-sample test on paired population mean differences
power.t.test(n = 5, d = 5, sd = 10 * sqrt(2 * (1 - 0.8)), sig.level = 0.05,
type = "paired", alternative = "one.sided")##
## Paired t test power calculation
##
## n = 5
## delta = 5
## sd = 6.325
## sig.level = 0.05
## power = 0.4296
## alternative = one.sided
##
## NOTE: n is number of *pairs*, sd is std.dev. of *differences* within pairs
## JG <- matrix(c(450, 20, 40, 40, 330, 40, 20, 40, 20), byrow = TRUE,
nrow = 3)
dimnames(JG) <- list(J1 = c("T", "F", "N"), J2 = c("T", "F", "N"))
print(JG)## J2
## J1 T F N
## T 450 20 40
## F 40 330 40
## N 20 40 20library(gmodels)
CrossTable(JG, expected = TRUE, prop.r = FALSE, prop.c = FALSE, prop.t = FALSE,
prop.chisq = FALSE, format = "SPSS")##
## Cell Contents
## |-------------------------|
## | Count |
## | Expected Values |
## |-------------------------|
##
## Total Observations in Table: 1000
##
## | J2
## J1 | T | F | N | Row Total |
## -------------|-----------|-----------|-----------|-----------|
## T | 450 | 20 | 40 | 510 |
## | 260.100 | 198.900 | 51.000 | |
## -------------|-----------|-----------|-----------|-----------|
## F | 40 | 330 | 40 | 410 |
## | 209.100 | 159.900 | 41.000 | |
## -------------|-----------|-----------|-----------|-----------|
## N | 20 | 40 | 20 | 80 |
## | 40.800 | 31.200 | 8.000 | |
## -------------|-----------|-----------|-----------|-----------|
## Column Total | 510 | 390 | 100 | 1000 |
## -------------|-----------|-----------|-----------|-----------|
##
##
## Statistics for All Table Factors
##
##
## Pearson's Chi-squared test
## ------------------------------------------------------------
## Chi^2 = 650.7 d.f. = 4 p = 1.609e-139
##
##
##
## Minimum expected frequency: 8
## library(vcd)
agreementplot(t(JG))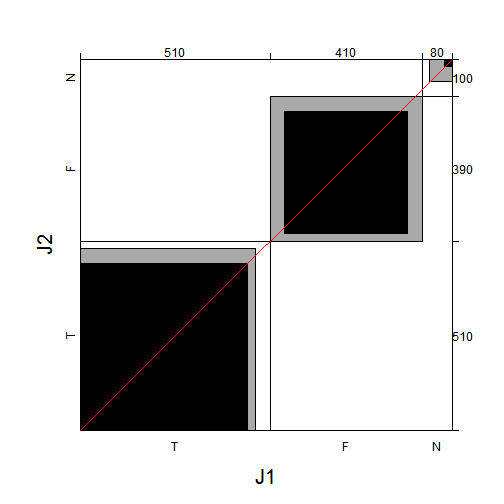
Plot of Agreement
summary(assocstats(as.table(JG)))##
## Number of cases in table: 1000
## Number of factors: 2
## Test for independence of all factors:
## Chisq = 651, df = 4, p-value = 2e-139
## X^2 df P(> X^2)
## Likelihood Ratio 753.96 4 0
## Pearson 650.74 4 0
##
## Phi-Coefficient : 0.807
## Contingency Coeff.: 0.628
## Cramer's V : 0.57
## data <- read.csv("Titanic.csv")
# who survived in the Titanic tragedy
library(ggplot2)
qplot(Class, data = data, geom = "bar", fill = Survived, postion = "stack",
facets = ~Sex) + coord_flip()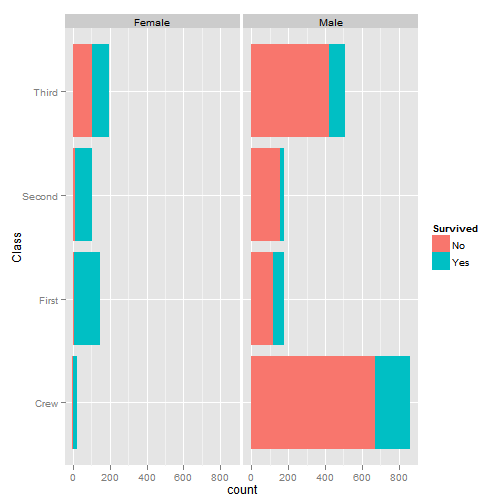
Plot of Facets
# survival rate
fun <- function(x) length(x[x == "Yes"])
t1 <- data.frame(with(data, aggregate(x = Survived, by = list(Class,
Sex, Age), FUN = length)))
t2 <- data.frame(with(data, aggregate(x = Survived, by = list(Class,
Sex, Age), FUN = fun)))
t1$y <- t2$x
t1$survived <- round(t1$y/t1$x, digits = 2)
t1[order(t1$survived, decreasing = T), ]## Group.1 Group.2 Group.3 x y survived
## 9 First Female Child 1 1 1.00
## 10 Second Female Child 13 13 1.00
## 12 First Male Child 5 5 1.00
## 13 Second Male Child 11 11 1.00
## 2 First Female Adult 144 140 0.97
## 1 Crew Female Adult 23 20 0.87
## 3 Second Female Adult 93 80 0.86
## 4 Third Female Adult 165 76 0.46
## 11 Third Female Child 31 14 0.45
## 6 First Male Adult 175 57 0.33
## 14 Third Male Child 48 13 0.27
## 5 Crew Male Adult 862 192 0.22
## 8 Third Male Adult 462 75 0.16
## 7 Second Male Adult 168 14 0.08# one-factor ANOVA
x <- factor(c(rep("B", 5), rep("A", 5), rep("P", 5)), level = c("B",
"A", "P"))
y <- c(35, 25, 73, 45, 22, 36, 45, 22, 33, 14, 66, 97, 90, 76, 71)
library(ggplot2)
qplot(x, y, geom = "boxplot", fill = x)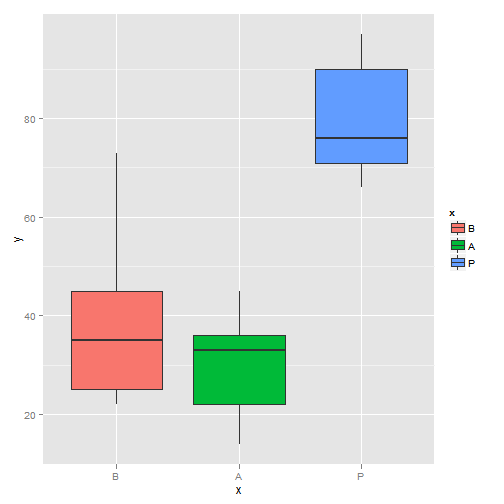
Boxplot (I)
summary(aov(y ~ x))## Df Sum Sq Mean Sq F value Pr(>F)
## x 2 7000 3500 14.2 0.00069 ***
## Residuals 12 2960 247
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 # two-factor ANOVA
T <- factor(rep(rep(1:2, c(5, 5)), 3))
levels(T) <- c("D", "N")
P <- factor(rep(1:3, c(10, 10, 10)))
levels(P) <- c("B", "A", "P")
y <- c(35, 25, 73, 45, 22, 31, 55, 36, 49, 44, 36, 45, 22, 33, 14,
65, 44, 75, 62, 54, 66, 97, 90, 76, 71, 90, 77, 55, 72, 76)
library(ggplot2)
qplot(P, y, geom = "boxplot", fill = T)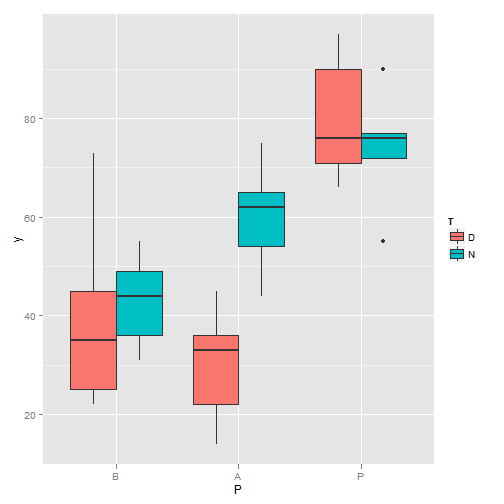
Boxplot (II)
qplot(T, y, geom = "boxplot", fill = P)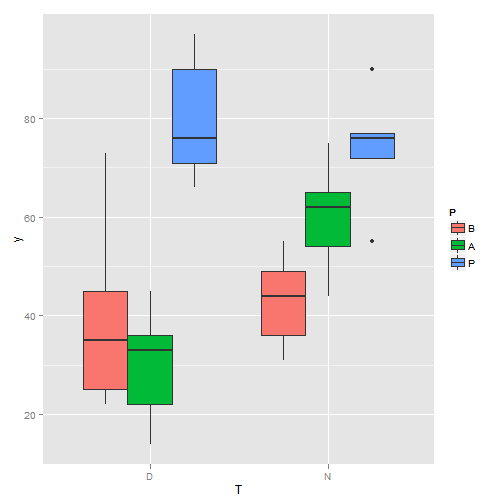
Boxplot(III)
summary(aov(y ~ T * P))## Df Sum Sq Mean Sq F value Pr(>F)
## T 1 608 608 3.23 0.085 .
## P 2 7655 3828 20.35 6.8e-06 ***
## T:P 2 1755 877 4.67 0.019 *
## Residuals 24 4514 188
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 myData <- data.frame(x = c(31, 25, 29, 20, 40, 32, 27, 33, 28, 21),
y = c(58, 52, 61, 57, 93, 63, 68, 71, 73, 48))
# linear
m1 <- lm(y ~ x, data = myData)
library(ggplot2)
qplot(x, y, data = myData, geom = c("point", "smooth"), method = "lm")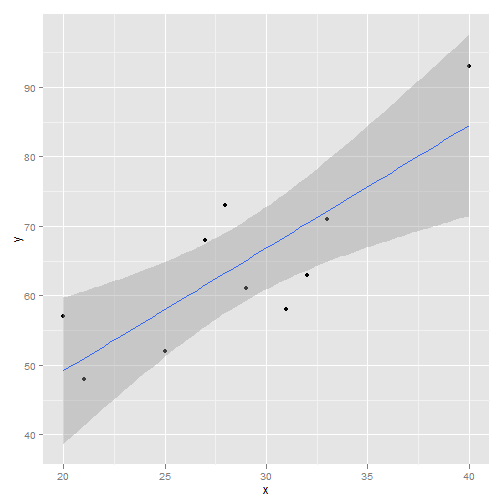
Plot of Linear Model
# log
m2 <- lm(y ~ log(x), data = myData)
# polynomial
m3 <- lm(y ~ poly(x, 2, raw = TRUE), data = myData)
# power
library(MASS)
bc <- boxcox(m1, plotit = FALSE)
lamda <- bc$x[which.max(bc$y)]
m4 <- lm(y ~ I(x^(1/lamda)), data = myData)
# exponential
f <- function(x, a, b) {
a * exp(b * x)
}
fm <- nls(y ~ f(x, a, b), data = myData, start = c(a = 10, b = 0.1))
m5 <- lm(y ~ I(coef(fm)[1] * exp(coef(fm)[2] * x)) + 0, data = myData)
anova(m1, m2, m3, m4, m5)## Analysis of Variance Table
##
## Model 1: y ~ x
## Model 2: y ~ log(x)
## Model 3: y ~ poly(x, 2, raw = TRUE)
## Model 4: y ~ I(x^(1/lamda))
## Model 5: y ~ I(coef(fm)[1] * exp(coef(fm)[2] * x)) + 0
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 8 499
## 2 8 582 0 -83
## 3 7 395 1 187 3.30 0.112
## 4 8 768 -1 -372 6.59 0.037 *
## 5 9 443 -1 325
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 AIC(m1, m2, m3, m4, m5)## df AIC
## m1 3 73.47
## m2 3 75.01
## m3 4 73.15
## m4 3 77.78
## m5 2 70.28myData <- read.csv("exData.csv")
m1 <- lm(W ~ purchase + Q + N, data = myData)
library(ggplot2)
qplot(c(Q, N), W, data = myData, geom = c("point", "smooth"), col = purchase,
method = "lm", xlab = "Q+N")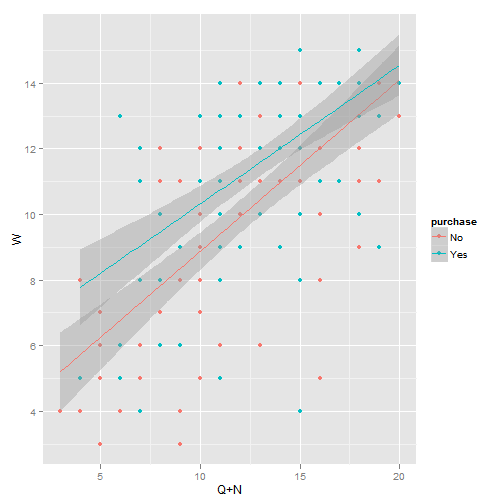
Plot of Linear Model
load("STOCK.RData")
# plot prices with volumes
opar = par(mar = c(5, 4, 4, 5) + 0.1)
barplot(STOCK$Volume, col = "Gray", border = NA, axes = FALSE, axisnames = FALSE,
ylim = c(0, 5e+08))
axis(4)
mtext("Volume", side = 4, line = 3)
par(new = TRUE)
plot(STOCK$Adjusted, main = "STOCK", yaxt = "n")
axis(2)
mtext("Price", side = 2, line = 3)
par(opar)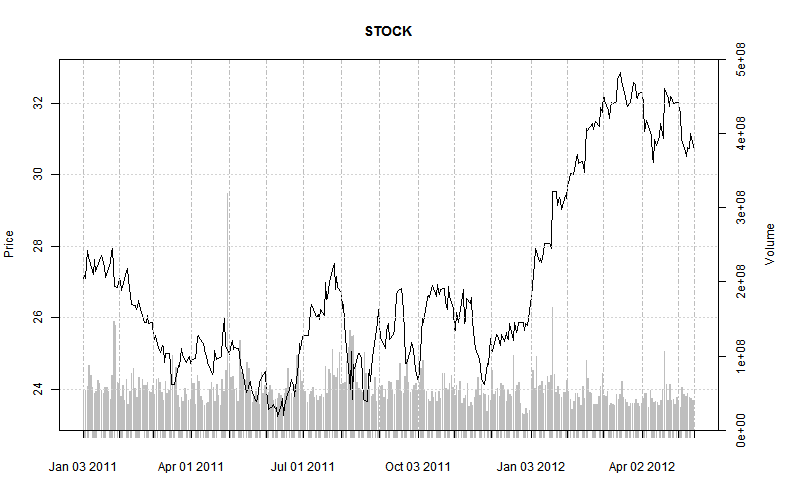
Plot of Time Series
# AR(3)
set.seed(1234)
n <- 200
x = arima.sim(model = list(ar = c(0.3, -0.7, 0.5), order = c(3, 0,
0)), n)
op <- par(mfrow = c(1, 2))
acf(x)
pacf(x)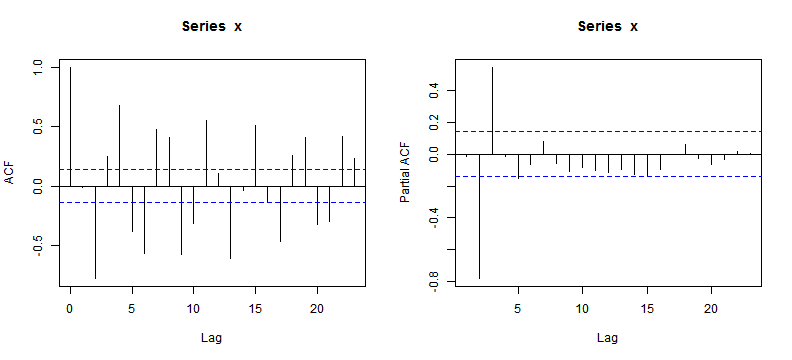
ACF and PACF Plot (I)
par(op)
Box.test(x, lag = log(n), type = "Ljung")##
## Box-Ljung test
##
## data: x
## X-squared = 261, df = 5.298, p-value < 2.2e-16
## y <- arima(x, order = c(3, 0, 0))
op <- par(mfrow = c(1, 2))
acf(y$resid)
pacf(y$resid)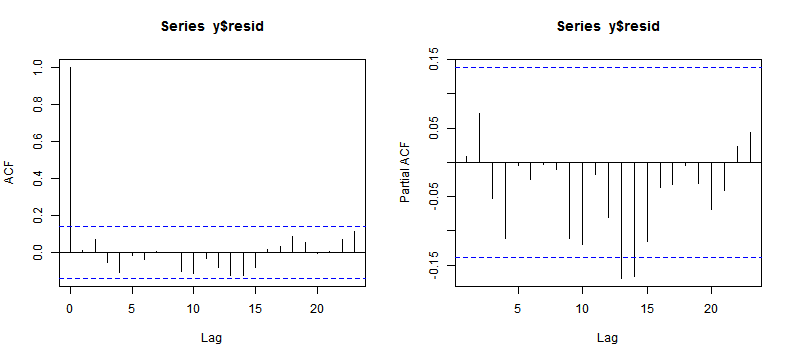
ACF and PACF Plot (II)
par(op)
confint(y)## 2.5 % 97.5 %
## ar1 0.27746 0.5101
## ar2 -0.82847 -0.6851
## ar3 0.42134 0.6516
## intercept -0.01366 0.3107library(forecast)
y <- auto.arima(x)
confint(y)## 2.5 % 97.5 %
## ar1 -0.271553 -0.1638
## ar2 -0.989699 -0.8908
## ma1 0.467648 0.7678
## ma2 0.358998 0.6902
## ma3 0.097702 0.3812
## intercept 0.002771 0.2938plot(forecast(y, h = 10, level = c(80, 95)))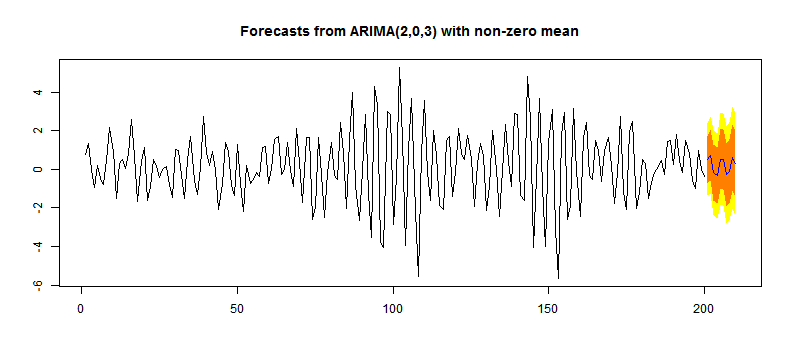
Time Series Plot with Forecasts
m1 <- lm(W ~ purchase + Q + N, data = myData)
set.seed(1234)
library(boot)
results <- boot(data = myData, statistic = bs, R = 1000, formula = W ~
purchase + Q + N)
plot(results, index = 2)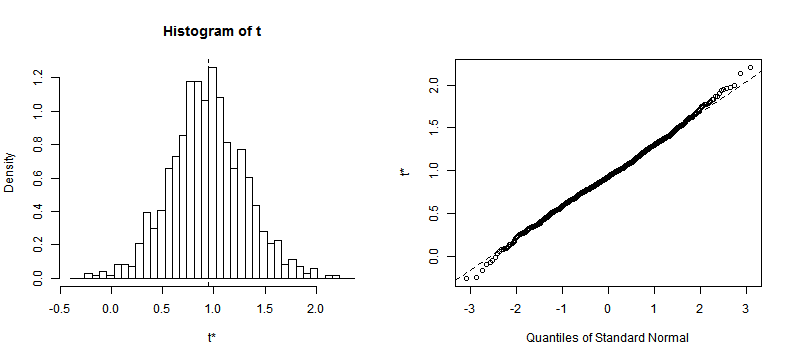
Density Plot and Q-Q Plot
confint(m1)## 2.5 % 97.5 %
## (Intercept) -0.61275 2.4117
## purchaseYes 0.22564 1.6733
## Q 0.08631 0.3343
## N 0.42732 0.7539boot.ci(results, type = "bca", index = 2)## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = results, type = "bca", index = 2)
##
## Intervals :
## Level BCa
## 95% ( 0.2749, 1.7697 )
## Calculations and Intervals on Original Scaleboot.ci(results, type = "bca", index = 3)## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = results, type = "bca", index = 3)
##
## Intervals :
## Level BCa
## 95% ( 0.1050, 0.3179 )
## Calculations and Intervals on Original Scaleboot.ci(results, type = "bca", index = 4)## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = results, type = "bca", index = 4)
##
## Intervals :
## Level BCa
## 95% ( 0.4037, 0.7934 )
## Calculations and Intervals on Original Scalecoef(m1)## (Intercept) purchaseYes Q N
## 0.8995 0.9495 0.2103 0.5906 print(results)##
## ORDINARY NONPARAMETRIC BOOTSTRAP
##
##
## Call:
## boot(data = myData, statistic = bs, R = 1000, formula = W ~ purchase +
## Q + N)
##
##
## Bootstrap Statistics :
## original bias std. error
## t1* 0.8995 -0.009424 0.77403
## t2* 0.9495 -0.013474 0.36631
## t3* 0.2103 -0.001269 0.05625
## t4* 0.5906 0.002895 0.09510print(sessionInfo(), locale = FALSE)## R version 2.14.2 (2012-02-29)
## Platform: i386-pc-mingw32/i386 (32-bit)
##
## attached base packages:
## [1] tcltk splines parallel grid stats graphics grDevices
## [8] utils datasets methods base
##
## other attached packages:
## [1] car_2.0-12 nnet_7.3-1 survival_2.36-12
## [4] quantmod_0.3-17 TTR_0.21-1 xts_0.8-6
## [7] Defaults_1.1-1 animation_2.0-6 boot_1.3-4
## [10] forecast_3.21 RcppArmadillo_0.3.0.3 Rcpp_0.9.10
## [13] fracdiff_1.4-1 tseries_0.10-28 zoo_1.7-7
## [16] quadprog_1.5-4 ggplot2_0.9.0 vcd_1.2-13
## [19] colorspace_1.1-1 MASS_7.3-17 gmodels_2.15.2
## [22] xtable_1.7-0 knitr_0.5
##
## loaded via a namespace (and not attached):
## [1] codetools_0.2-8 dichromat_1.2-4 digest_0.5.2
## [4] evaluate_0.4.2 formatR_0.4 gdata_2.8.2
## [7] gtools_2.6.2 highlight_0.3.1 lattice_0.20-6
## [10] memoise_0.1 munsell_0.3 parser_0.0-14
## [13] plyr_1.7.1 proto_0.3-9.2 RColorBrewer_1.0-5
## [16] reshape2_1.2.1 scales_0.2.0 stringr_0.6
## [19] tools_2.14.2